• 1 逆元定义
• 2 欧几里得算法（求最大公约数）
• 3 扩展欧几里得算法
  • 3.1 预备知识
  • 3.2 关于扩展欧几里得算法
  • 3.3 模板
  • 3.4 算法推导过程
  • 3.5 利用拓展欧几里得算法求逆元
• 4 费马小定理
  • 4.1 定义
  • 4.2 模板
• 5 欧拉定理
• 6 RSA公钥密码经典例题
  • 6.1 题目描述
  • 6.2 分析
  • 6.3 题解
• References

前两天二刷了《模仿游戏》，Alan Turing 在二战中研制的图灵机破译了德军号称牢不可破的 Enigma 密码机。这部剧让我对计算机产生了一些新的理解，结合以前修过的密码学原理课程，因此想记录一下之前没掌握好的数论知识，并且以 RSA 公钥密码为例，解一道经典题。

1 逆元定义

若 $a\ *\ x\ ≡\ 1\ (mod\ b)$ ，且 a 与 b 互斥，那么就能定义 x 为 a 的逆元，记为 $a^{-1}$，也可称为 x 为 a 的倒数。

2 欧几里得算法（求最大公约数）

首先介绍古老而又强大的欧几里得算法（又称辗转相除法）：
两个数 a 和 b 的最大公因子（greatest common divisior）是能整除它们两者的最大整数。欧几里德算法用于计算两个整数 a，b 的最大因子。记 gcd(a, b) 为自然数 a 与 b 的最大公因子。特别的，有 gcd(0, n) = 0，因为任何整数都能整除 0。

内容：

代码：

int gcd(int a, int b){   
    return b == 0 ? a : gcd(b, a % b);     
}

3 扩展欧几里得算法

3.1 预备知识

1. 取模运算：

(a + b) % c = (a % c + b % c) % c
(a * b) % c = (a % c * b % c) % c

取模运算对除法不成立，当要求 (a / b) % c 时，可转化为逆元来求：

这就是逆元的作用。

2. 裴蜀定理：

给予两个整数 a，b，必存在整数 x，y 使得

即如若 $ax+by=c$ 有解，那么有 $gcd(a,\,b)\,|\,c$（c 一定是 $gcd(a,\,b)$ 的若干倍）

特例：当 $c = 1$ 时，如果 $ax+by=1$ 有解，那么 $gcd(a,\,b)\,=\,1$

3.2 关于扩展欧几里得算法

• 扩展欧几里得算法（Extended Euclidean algorithm）是欧几里得算法的扩展。它可用来求解形如 $ax+by=c\,(a,b,c\,\in Z)$ 方程的一组整数解。

• 对于求解方程 $ax+by=c\,(gcd(a,\,b)\,|\,c)$ ，只需求解出方程

  $$ax+by=gcd(a,\,b)$$
  的一组解，将 $x,y$ 分别乘上 $\frac {c}{gcd(a,b)}$ 即可得到方程 $ax+by=c\,(gcd(a,\,b)\,|\,c)$ 的一组解。

• 扩展欧几里得算法可以用来计算模反元素(也叫模逆元)，而模反元素在 RSA 加密算法中有举足轻重的地位。

3.3 模板

(思考了一下该先放模板，还是先放算法的证明过程，最后决定先放模板，然后就着模板理解算法的证明过程)

ll ex_gcd(ll a, ll b, ll &x, ll &y){
    //标记1
    if(b == 0){
        x = 1, y = 0;
        return a;
    }
    ll d = ex_gcd(b, a % b, x, y);
    ll temp = y;
    //标记2
    y = x - (a / b) * y;
    x = temp;
    //标记3
    return d;
}

3.4 算法推导过程

现有方程：

$$ ax+by=gcd(a,\,b) $$

记 ex_gcd(a, b, x, y) 为求解上述方程的函数，函数返回的是 $gcd(a,b)$ 的最大公约数(对应模板代码标记3），其中形参 $x,y$ 为引用参数(全局变量)，也是上述方程的解。

1. 边界情况(对应模板代码标记1）：
   当 $b=0$ 时，方程为 $ax=gcd(a,0)$ ，解得

   $$ \left\{ \begin{array}{l} x=1 \\ y=0 \end{array} \right. $$

   此时 a 就是 $gcd(a,0)$ 的最大公约数，因此函数return a。

2. 一般情况(对应模板代码标记2）：
   当 $b\neq0$ 时，有欧几里得算法

   $$ gcd(a\,,b)\,=\,gcd(b^\prime\,,\,a^\prime\,\%\,b^\prime) $$

   则有方程

   $$ ax+by=gcd(a,\,b)=gcd(b^\prime\,,\,a^\prime\,\%\,b^\prime) $$

   另外有等式（不是啥公式，一个运算技巧）：

   $$ a\,\%\,b=a-(a/b)*b $$

   则方程可化为

   $$ gcd(b^\prime\,,\,a^\prime\,\%\,b^\prime)=b^\prime x^\prime+(a^\prime\,\%\,b^\prime)y^\prime=b^\prime x^\prime+(a^\prime-(a^\prime/b^\prime)*b^\prime)y^\prime $$

   上式化简得：

   $$ b^\prime x^\prime+a^\prime y^\prime-(a^\prime / b^\prime)*b^\prime*y^\prime=a^\prime y^\prime+b^\prime*(x^\prime-a^\prime /\,b^\prime*y^\prime) $$

   于是可以得到关于方程解 $x,y$ 的递推关系：

   $$ \left\{ \begin{array}{l} x=y^\prime \\ y=x^\prime-a^\prime /\,b^\prime*y^\prime \end{array} \right. $$

3. 由此我们得到了边界条件以及递归式，即每次递归ex_gcd(b, a mod b, x, y)，稍加处理，即可求得方程 $ax+by=gcd(a,\,b)$ 的一组解 $x,y$ 。

3.5 利用拓展欧几里得算法求逆元

那么问题来了，我们通过函数ex_gcd(a, b, x, y)，求得 $gcd(a,b)$（即最大公约数）的结果，以及一组方程解 $(x,y)$，对求逆元有什么作用？

1. 根据逆元定义 $a\,*\,x\,≡\,1\,(mod\,b)$
   当我们求 $a$ 在 $mod\,b$ 情况下的逆元时，假设逆元为 x ，即
   

   $$ ax\equiv1(mod\,b) $$

   转化等式：

   $$ ax\equiv1+by(\,\,(b * y)|(a *x),\ 即\ a * x\ 是\ b * y\ 的若干倍) $$

   移项
   

   $$ ax+by\equiv1 $$

   则最小的 $x$ 即为 $a$ 在 $mod\,b$ 情况下的一个逆元。

2. 由裴蜀定理：

   $$ ax+by=gcd(a,\,b) $$

   当 $gcd(a,\,b)=1$ 时，由扩展欧几里得函数ex_gcd(a, b, x, y)求得的方程解 $x$ 即为我们所求的最小乘法逆元。

3. 因此下面代码中的标记4得到解释：

//拓展欧几里得算法
ll ex_gcd(ll a, ll b, ll &x, ll &y){
    //标记1
    if(b == 0){
        x = 1, y = 0;
        return a;
    }
    ll d = ex_gcd(b, a % b, x, y);
    ll temp = y;
    //标记2
    y = x - (a / b) * y;
    x = temp;
    //标记3
    return d;
}

//求a在mod下的逆元x
ll getInv(ll a, ll mod){
    ll x, y;
    ll d = ex_gcd(a, mod, x, y);
    //标记4
    return d == 1 ? (x + mod) % mod : -1;
}

• 当扩展欧几里得函数ex_gcd(a, b, x, y)返回的最大公约数 $d = 1$ 时，$x$ 即为 $a\,mod\,b$ 下的最小乘法逆元，(x + mod) % mod是为了将 $x$ 调整到 0 ~ (b - 1)的范围中；
• 当函数的返回值 $d\neq 1$ 时，即说明逆元不存在，返回 $-1$；
• 拓展欧几里得求逆元的时间复杂度：$O(logn)$；
• 适用范围：只要存在逆元即可求，适用于个数不多但是 mod 很大的时候，也是最常见的一种求逆元的方法；

4 费马小定理

4.1 定义

如果 $p$ 是一个质数，且整数 $a$ 不是 $p$ 的倍数，则有：$a^{p-1}\equiv1(mod\,p)$

• 由公式得：

  $$ a^{p-2}\,*\,a\equiv1(mod\,p) $$

  因此 $a^{p-2}$ 即为 $a$ 在 $mod\,p$ 意义下的逆元。

• 而 $a^{p-2}$ 可用快速幂求解（关于快速幂原理可在此博客了解：快速幂 & 快速乘原理讲解（模板））

4.2 模板

//快速幂
ll ksm(ll a, ll p, ll mod) {
    ll ans = 1, base = a % mod;
    while(p) {
        if(p & 1) {
            ans = (ans * base) % mod;
        }
        base = (base * base) % mod;
        p >>= 1;
    }
    return ans;
}
//求逆元
ll getInv(ll a, ll mod){
    return ksm(a, p - 2, mod);
}

• 费马小定理求逆元的时间复杂度：$O(logmod)$
• 适用范围：根据费马小定理，$mod\,p$ 为质数时适用。并且比扩展欧几里得算法好写一些。

5 欧拉定理

欧拉定理（也称费马-欧拉定理），是一个关于同余的性质。欧拉定理表明，若 $p,\,a$ 为正整数，且 $p,\,a$ 互质，则：

$$ a^{\varphi (p)}\equiv1(mod\ p) $$

• 由公式得：

  $$ a^{\varphi (p)-1}\,*\,a\equiv1(mod\,p) $$

  因此 $a^{\varphi (p)-1}$ 即为 $a$ 在 $mod\,p$ 意义下的逆元。

• 可以看到，费马小定理是欧拉定理的特例，当 $p$ 为质数时，$\varphi (p)=\,p-1$，$\varphi (p)-1=\,p-2$

• 欧拉定理比费马小定理适用范围更广，因为模数 $p$ 可以不是质数。

• 一般很少有人直接用欧拉定理求逆元（偷个懒，板子就不贴上来了）

6 RSA公钥密码经典例题

说了这么多废话 （正经话），终于可以开始做题了。

6.1 题目描述

RSA 是一种经典的加密算法。它的基本加密过程如下：
首先生成两个质数 $p, q$，令 $n = p * q$，设 $d$ 与 $(p - 1) * (q - 1)$ 互质，则可找到 $e$ 使得 $d * e$ 除 $(p - 1) * (q - 1)$ 的余数为 1。
$n, d, e$ 组成了私钥，$n, d$ 组成了公钥。
当使用公钥加密一个整数 $X$ 时(小于 $n$ )，计算 $C = X^{d}\,mod\,n$ ，则 $C$ 是加密后的密文。
当收到密文 $C$ 时，可使用私钥解开，计算公式为 $X=C^{e}\,mod\,n$。
例如，当 $p = 5, q = 11, d = 3$ 时，$n = 55,\,e = 27$。
若加密数字 $24$ ，得 $24^{3}\,mod\,55 = 19$ 。
解密数字 $19$ ，得 $19^{27}\,mod\,55 = 24$ 。
现在你知道公钥中 $n = 1001733993063167141, \,d = 212353$，同时你截获了别人发送的密文 $C = 20190324$ 。请问：原文是多少?

6.2 分析

• 由题目已知 $n,\,d,\,C\,$ ，根据解密公式 $X=C^{e}\,mod\,n$，只需求得私钥 $e$ ，即可解得原文 $X$。

• 根据题目信息：$d$ 与 $(p-1)*(q-1)$ 互质，则可找到 $e$ 使得 $d * e$ 除 $(p - 1) * (q - 1)$ 的余数为 1，翻译成 人话（公式）就是：

  $$ d * e\equiv1(mod\,\,(p - 1) * (q - 1)\,) $$

• 设 $k = (p - 1) * (q - 1)$，即：

  $$ d\,*\,e\equiv1(mod\,k) $$

• 由上述公式可得 $e$ 即为 $d$ 在 $mod\,k$意思下的乘法逆元。在这里我们用拓展欧几里得算法求解。

• 最后一个问题：关于 $k$ 即$(p - 1) * (q - 1)$应该如何求解。这里用到质因数分解，由题目可知 $n = p * q$，且 $p,\,q$ 均为质数。我们先找到一个小于 $n$ 的质数 $p$，再用 $n / p$ 即可得到 $q$ 。

6.3 题解

#include <iostream>
#include <cstdio>
using namespace std;

typedef long long ll;

ll n = 1001733993063167141, d = 212353, c = 20190324;

//判断质数 
ll isPrime(ll x){
    for(ll i = 2;i <= x;i++){
        if(x % i == 0){
            return i;
        }
    }
}

//扩展欧几里得算法 
ll ex_gcd(ll a, ll b, ll &x, ll &y){
    if(b == 0){
        x = 1, y = 0;
        return a;
    }
    ll d = ex_gcd(b, a % b, x, y);
    ll temp = y;
    y = x - (a / b) * y;
    x = temp;
    return d;
}

//求a在mod下的乘法逆元x
ll getInv(ll a, ll mod){
    ll x, y;
    ll d = ex_gcd(a, mod, x, y);
    return d == 1 ? (x + mod) % mod : -1;
}

//快速乘 
ll ksc(ll a, ll b, ll mod) {
    ll ans = 0;
    while(b) {
        if(b & 1) {
            ans = (ans + a) % mod;
        }
        a = (a + a) % mod;
        b >>= 1;
    }
    return ans;
}

//快速幂 
ll ksm(ll a, ll b, ll mod) {
    ll ans = 1, base = a;
    while(b) {
        if(b & 1) {
            ans = ksc(ans, base, mod) % mod;
        }
        base = ksc(base, base, mod) % mod;
        b >>= 1;
    }
    return ans;
}

int main(){
    ll p = isPrime(n), q = n / p, k = (p - 1) * (q - 1);
    ll e = getInv(d, k);
    //	printf("e is %lld\n", e);
    ll x = ksm(c, e, n);
    printf("%lld\n", x);
    return 0;
}

• 注意到题目中的数据实在是太大了，单独用快速幂求解 $X=C^{e}\,mod\,n$ 会导致数据溢出，因此我们对快速幂优化了一下（用快速乘求每次 $a$ 的余数，再快速幂对余数进行幂运算），达到模拟大数模幂运算的效果。

• 相关博客可参考：快速幂 & 快速乘取模（模拟大数模幂运算，解决乘法爆long long问题）

运算结果：

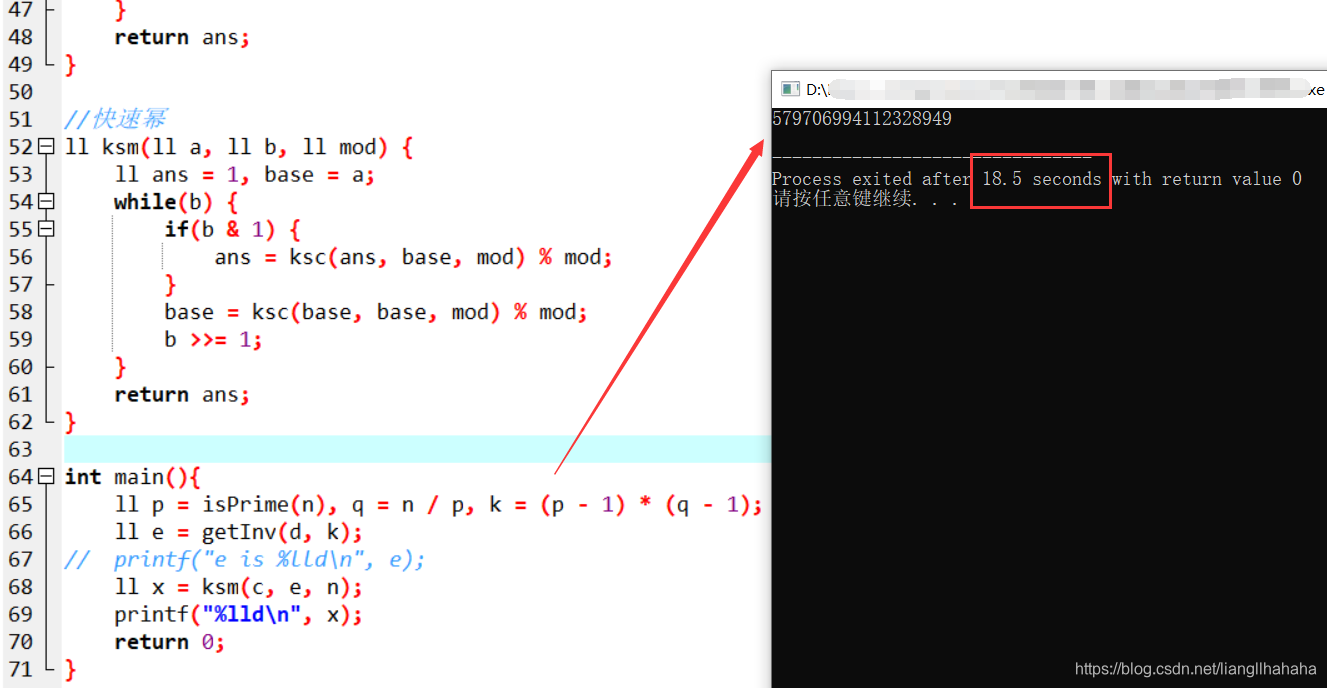
• 答案：579706994112328949
• RSA 是非对称加密算法，基于大数分解，题目只是模拟了一下 RSA 解密的过程，可以看到当 $n = 1001733993063167141$ 时，我的电脑跑出结果就花了十几秒。而真正 RSA 密码中，$n$ 一般而言可达到 $1024\sim2048$ 比特，普通的计算机跑出结果要十年左右，量子计算机需一周。

References

• 欧几里德算法与扩展欧几里德算法