快速幂 && 快速乘取模(模拟大数模幂运算,解决乘法爆long long问题)
引言
在 RSA 密码中,当收到密文 C 时,可使用私钥解开,计算公式为
$$ X\ =\ C^{e}\ mod\ n $$
如果想让你计算$$ 20190324^{823816093931522017}\ mod\ 1001733993063167141 $$应该如何用代码实现?我们知道,在 Java 里有大数类,Python 依靠其强大的计算性能有些数据甚至可以直接计算。那么在 C/C++ 中应该如何处理?单独用快速幂也会爆 long long ,我们可以采取快速幂调用快速乘进行取模的方法得到结果。
关于快速幂与快速乘的具体原理,可在此博客了解:快速幂 & 快速乘原理讲解(模板)
1 原因分析
首先我们直接用快速幂计算引言中提到的公式:
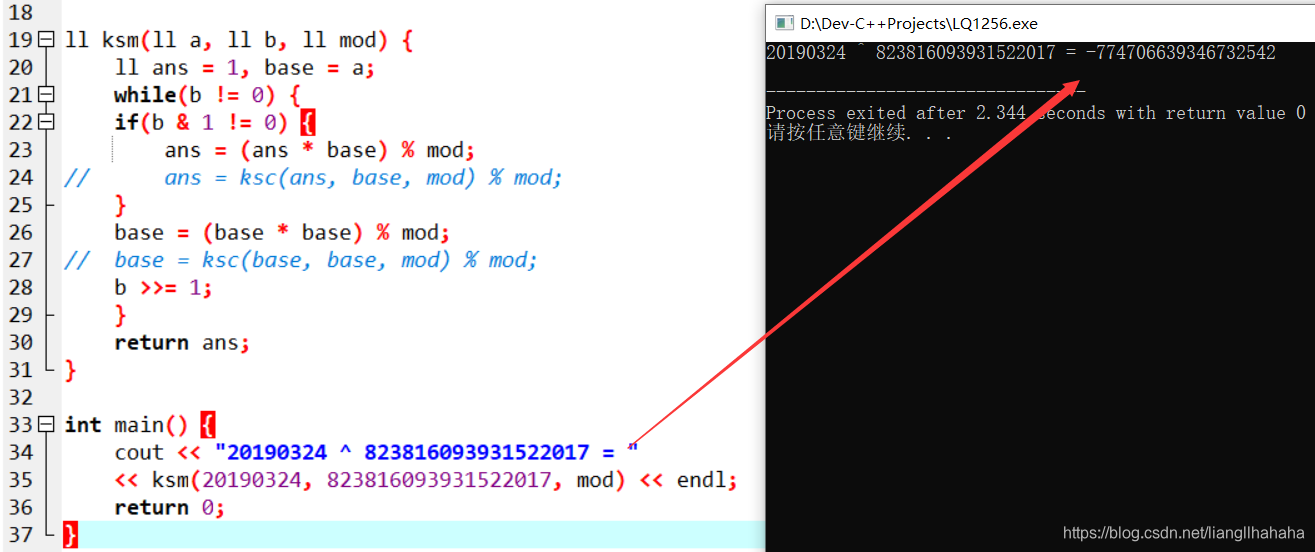
不出意料,结果直接溢出。
2 快速幂取模(大数模幂模拟)
因为数据实在是太大了,取模和开 long long 也没办法解决问题,于是可以对快速幂中的乘法运算
ans = (ans * base) % mod;
base = (base * base) % mod;
进行优化,改为快速乘求结果
ll ksc(ll a, ll b, ll mod) {
ll ans = 0;
while(b) {
if(b & 1) {
ans = (ans + a) % mod;
}
a = (a + a) % mod;
b >>= 1;
}
return ans;
}
ll ksm(ll a, ll b, ll mod) {
ll ans = 1, base = a;
while(b) {
if(b & 1) {
//优化1
ans = ksc(ans, base, mod) % mod;
}
//优化2
base = ksc(base, base, mod) % mod;
b >>= 1;
}
return ans;
}
3 验证
完整代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1001733993063167141;
ll ksc(ll a, ll b, ll mod) {
ll ans = 0;
while(b) {
if(b & 1) {
ans = (ans + a) % mod;
}
a = (a + a) % mod;
b >>= 1;
}
return ans;
}
ll ksm(ll a, ll b, ll mod) {
ll ans = 1, base = a;
while(b) {
if(b & 1) {
ans = ksc(ans, base, mod) % mod;
}
base = ksc(base, base, mod) % mod;
b >>= 1;
}
return ans;
}
int main() {
cout << "20190324 ^ 823816093931522017 = " << ksm(20190324, 823816093931522017, mod) << endl;
return 0;
}
运行结果:
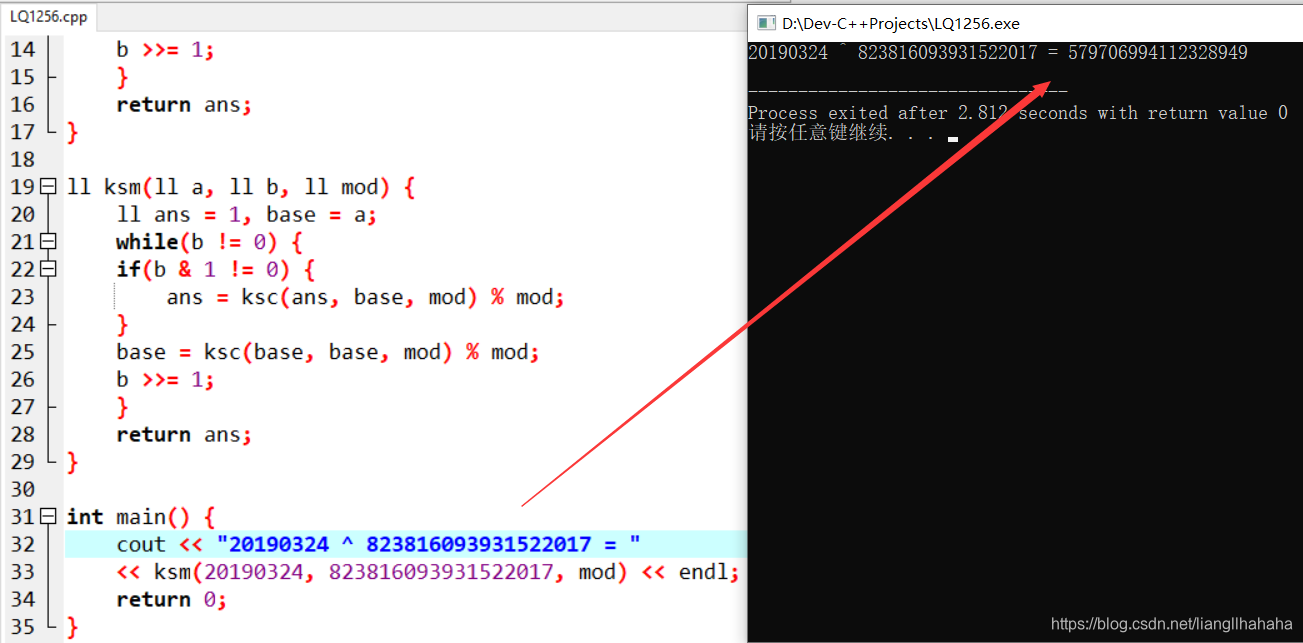
可以看到数据溢出的问题得到解决,达到了大数模拟的效果。