1 Dijkstra算法
适用范围:不能解决带有负边的图
1.1 算法模板
#include <iosream>
#include <cstdio>
using namespace std;
#define maxn 205
#define inf 1e18
#define eps 0.00001
typedef long long ll;
const ll mod = 1e9 + 7;
const double pi = acos(-1);
ll n, vis[maxn][maxn], dis[maxn];
bool flag[maxn];
void dij() {
ll now = 1;
for(ll i = 2; i <= n; i++) {
dis[i] = inf;
}
flag[1] = 1;
for(ll i = 1; i <= n; i++) {
ll temp = inf;
//找到当前轮次最小的dis[j]顶点即为now
for(ll j = 1 ; j <= n; j++) {
if(flag[j] == 0 && dis[j] < temp) {
temp = dis[j];
now = j;
}
}
flag[now] = 1;
//更新与now相连顶点的dis值
for(ll j = 1; j <= n; j++){
dis[j] = min(dis[j], dis[now] + vis[now][j]);
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for(ll i = 1; i <= n; i++){
for(ll j = 1; j <= n; j++){
vis[i][j] = inf;
}
}
for(ll i = 1; i <= n - 1; i++) {
for(ll j = 1; j <= n - i; j++) {
ll temp;
cin >> temp;
vis[i][i + j] = temp;
if(i == j){
vis[i][j] = 0;
}
}
}
dij();
cout << dis[n] << endl;
return 0;
}
1.2 例题
题目链接:1003 Emergency (25分)
Problem Description
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification
Each input file contains one test case. For each test case, the first line contains $4$ positive integers: $N (≤500)$ - the number of cities (and the cities are numbered from $0$ to $N−1$), $M$ - the number of roads, $C1$ and $C2$ - the cities that you are currently in and that you must save, respectively. The next line contains $N$ integers, where the i-th integer is the number of rescue teams in the $i$-th city. Then $M$ lines follow, each describes a road with three integers $c1$, $c2$ and $L$, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from $C1$ to $C2$.
Output Specification
For each test case, print in one line two numbers: the number of different shortest paths between $C1$ and $C2$, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output
2 4
题目大意
给出 $N$ 个城市,及每个城市的救援队数量,你在 $C1$ 点,需要去救援 $C2$ 点,目标是找出权重最小的不同路径数及能召集到最多救援队的数量。
解题思路
用 $Dijkstra$ 求出最小路径数,并增加救援队数量以及不同路径数的条件判断即可。
题解
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 510, INF = 0X3f3f3f3f;
//城市救援队数量,不同的路径数,边的权重
int arr[maxn] = {0}, ans[maxn], num[maxn], cost[maxn][maxn], dis[maxn], vis[maxn];
int n, m, c1, c2;
void dij(){
//初始化
dis[c1] = 0;
num[c1] = arr[c1];
ans[c1] = 1;
for(int i = 0;i < n;i++){
int now, temp = INF;
for(int j = 0;j < n;j++){
if(!vis[j] && dis[j] < temp){
temp = dis[j];
now = j;
}
}
//找到最小距离
vis[now] = 1;
for(int j = 0;j < n;j++){
//如果遍历的顶点与找到最小距离的顶点重复,跳过,否则答案有误
if(j == now){
continue;
}
//最短距离相同时,累加
if(dis[j] == dis[now] + cost[now][j]){
ans[j] += ans[now];
num[j] = max(num[j], num[now] + arr[j]);
}
if(dis[j] > dis[now] + cost[now][j]){
dis[j] = dis[now] + cost[now][j];
ans[j] = ans[now];
num[j] = num[now] + arr[j];
}
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
#ifdef ONLINE_JUDGE
#else
freopen("input.txt", "r", stdin);
#endif
memset(dis, INF, sizeof(dis));
memset(vis, 0, sizeof(vis));
memset(num, 0, sizeof(num));
memset(ans, 0, sizeof(ans));
cin >> n >> m >> c1 >> c2;
for(int i = 0;i < n;i++){
cin >> arr[i];
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(i == j)
cost[i][j] = 0;
else
cost[i][j] = INF;
}
}
for(int i = 0;i < m;i++){
int a, b, l;
cin >> a >> b >> l;
cost[a][b] = cost[b][a] = l;
}
dij();
cout << ans[c2] << " " << num[c2];
return 0;
}
2 BellmanFord
2.1 讲解
-
适用范围
- BellmanFord 算法适合含有负权的大图求最短路径 。
- 但如果存在从源点可达的负权值回路(负回路),则最短路径不存在。因为可以重复走这个回路,使得路径无穷小。
-
松弛操作
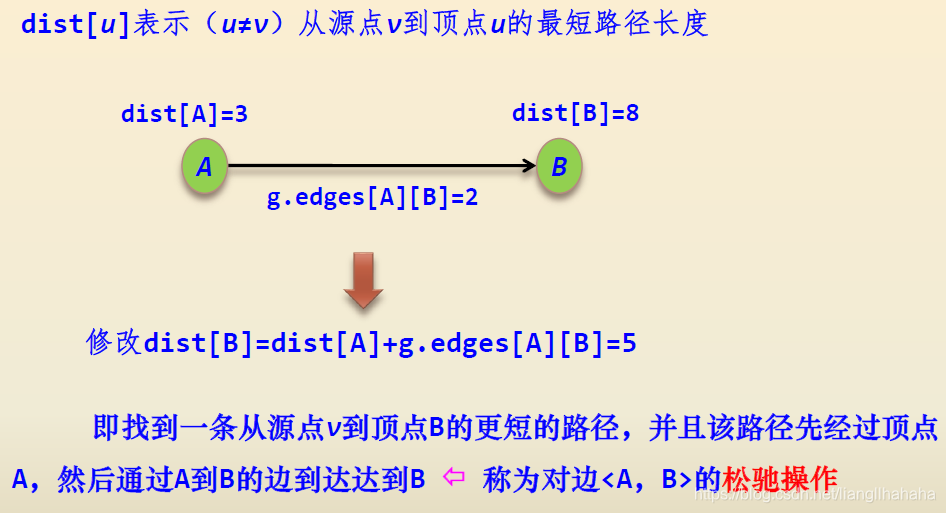
2.2 例题
问题描述
给定一个 n 个顶点,m 条边的有向图(其中某些边权可能为负,但保证没有负环)。请你计算从 1 号点到其他点的最短路(顶点从 1 到 n 编号)。
输入格式
第一行两个整数 n, m。
接下来的 m 行,每行有三个整数 u, v, l,表示 u 到 v 有一条长度为 l 的边。
输出格式
共 n - 1 行,第 i 行表示 1 号点到 i + 1 号点的最短路。
样例输入
3 3
1 2 -1
2 3 -1
3 1 2
样例输出
-1
-2
数据规模与约定
对于 10% 的数据,n = 2,m = 2。
对于 30% 的数据,n <= 5,m <= 10。
对于 100% 的数据,1 <= n <= 20000,1 <= m <= 200000,-10000 <= l <= 10000,保证从任意顶点都能到达其他所有顶点。
解题思路
求图的最短路径,但是图中有负边,且图的规模很大,因此考虑使用 $Bellman-Ford$ 算法。
题解
#include <iostream>
#include <cstdio>
using namespace std;
const int INF = 0x3f3f3f;
const int maxn = 200005;
int u[maxn], v[maxn], w[maxn], dis[maxn], path[maxn];
int main(){
int n, m;
cin >> n >> m;
for(int i = 1;i <= m;i++){
cin >> u[i] >> v[i] >> w[i];
}
for(int i = 1;i <= n;i++){
dis[i] = INF;
}
//将一号顶点置为0
dis[1] = 0;
//从 dist(0)[u] 递推出 dist(n-1)[u] 循环n-1次
for(int i = 1;i <= n - 1;i++){
int flag = 0;
for(int x = 1;x <= n;x++){
path[x] = dis[x];
}
for(int j = 1;j <= m;j++){
//顶点到 v[j]顶点的路径 > u[j]顶点到 v[j] 的距离 + u[j]到 v[j]边的权值
if(dis[v[j]] > dis[u[j]] + w[j]){
dis[v[j]] = dis[u[j]] + w[j];
}
}
for(int a = 1;a <= n;a++){
if(path[a] != dis[a]){
flag = 1;
break;
}
}
if(!flag){
break;
}
}
for(int i = 2;i <= n;i++){
printf("%d\n", dis[i]);
}
return 0;
}