1 问题描述
我们发现,在 $int$ 型下使用 $pow$ 函数求 $5^{3}$,结果为 $124$ 。
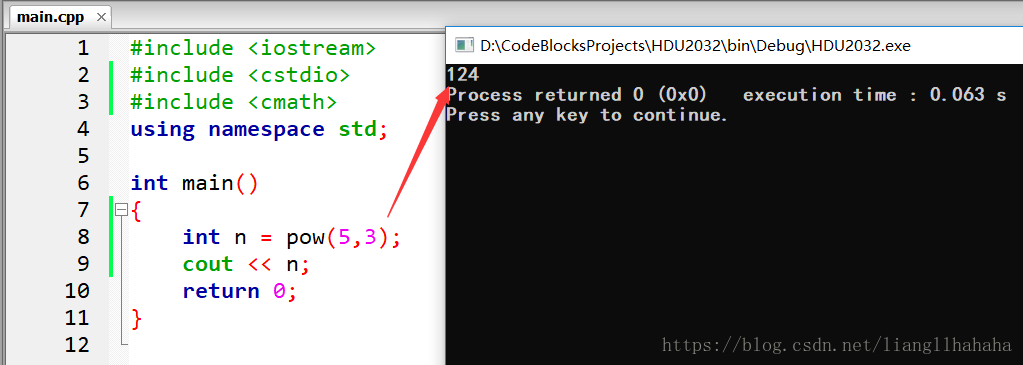
2 原因分析
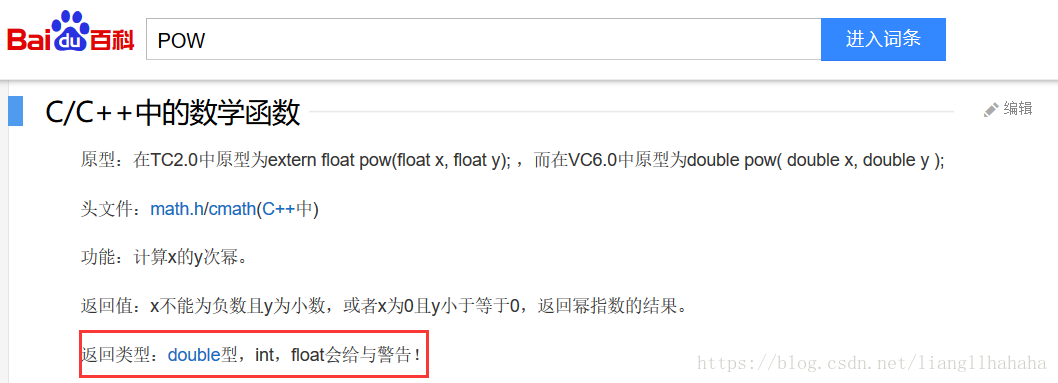
$pow$ 函数的返回值为
double型 ,因浮点数长度问题,存在截断误差。
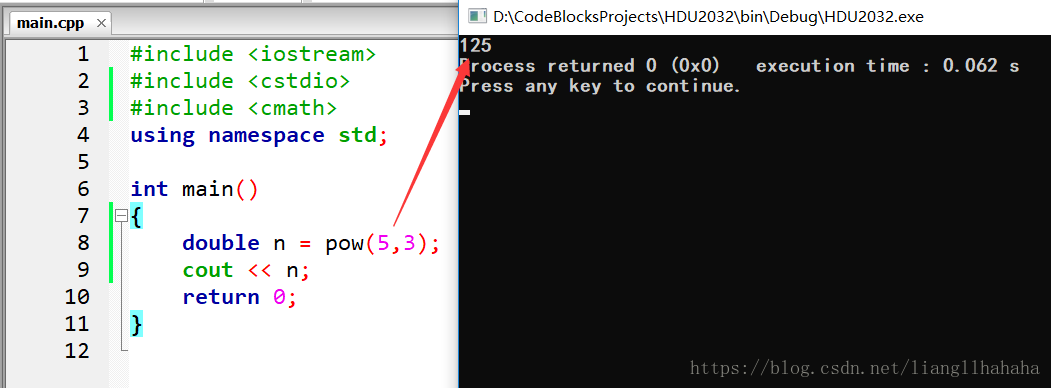
3 解决方法
将变量定义为
double型
有没有更快求幂的方法?
4 快速幂讲解
假设我们要求 $a^{b}$ ,按照朴素算法就是把 a 连乘 b 次,这样一来时间复杂度是 $O(b)$ ,即是 $O(n)$ 级别。但快速幂能做到 $O(logn)$ 的复杂度。
快速幂:

对于二进制的位运算,我们需要用到 & 与 >> 运算符,详见 位运算符的应用
先上实现快速幂运算的具体代码:
long long ksm(long long a, long long b) {
long long ans = 1, base = a;
while(b != 0) {
if(b & 1 != 0) {
ans *= base;
}
base *= base;
b >>= 1;
}
return ans;
}
其中 b & 1 指取 b 的二进制数的最末位,如 11 的二进制数为 1011 ,第一次循环,取的是最右边的 1 ,以此类推。
而 b >>= 1 等效于 b = b >> 1,即右移 1 位,删去最低位。
以 $a ^ {11}$ 为例:
b 的二进制数为 1011,二进制从右向左算,但乘出来的顺序是 $a^{2^{0}} * a^{2^{1}} * a^{2^{3}}$ ,是从左向右的。我们不断的让 $base\,*=\,base$ 目的是累乘,以便随时对 ans 做出贡献。
要理解 $base*=base$ 这一步:因为 $base\,*\,base == base^{2}$,下一步再乘,就是 $base^{2} * base^{2} == base^{4}$,然后同理 $base^{4} * base^{4} == base^{8}$,由此可以做到 $base→ base^{2} → base^{4} → base^{8} → base^{16} → base^{32}$ … 指数正好是 $2^{i}$。再看上面的例子,$a^{11} = a^{1}\,*\,a^{2}\,*\,a^{8}$ ,这三项就可以完美解决了,快速幂就是这样。
如还有不明白的地方,建议手动模拟代码的运行过程。
5 快速乘讲解
我们知道,在计算机中做加法运算会比乘法快得多(参考模电中的加法器),做乘法运算往往会溢出,即使用 long long 类型也拯救不了。因此需要寻找一种能高效完成乘法运算且不会溢出的算法,这就是快速乘算法。
快速乘与快速幂原理相似,也是将运算转换为二进制处理.
以 $a * 11$ 为例: 11 的二进制数为 1011,则有 $a * 11 = a * 2^{0}\,+\,a * 2^{1}\,+\,a * 2^{3}$
就是把快速幂中的 * 号改为 + 号
long long ksc(long long a, long long b) {
long long ans = 0;
while(b != 0) {
if(b & 1 != 0) {
ans += a;
}
a += a;
b >>= 1;
}
return ans;
}
此版本的复杂度和快速幂一样,也是 $O(logn)$ 。如果需要特别卡常数,可以去了解 $O(1)$ 版本的快速乘。
6 完整代码
为了防止溢出,一般快速幂和快速乘的算法会在 $mod$ 下运用,下面给出取模运算代码。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e7;
//a ^ b
ll ksm(ll a, ll b, ll mod) {
ll ans = 1, base = a;
while(b != 0) {
if(b & 1 != 0) {
ans = (ans * base) % mod;
}
base = (base * base) % mod;
b >>= 1;
}
return ans;
}
//a * b
ll ksc(ll a, ll b, ll mod) {
ll ans = 0;
while(b != 0) {
if(b & 1 != 0) {
ans = (ans + a) % mod;
}
a = (a + a) % mod;
b >>= 1;
}
return ans;
}
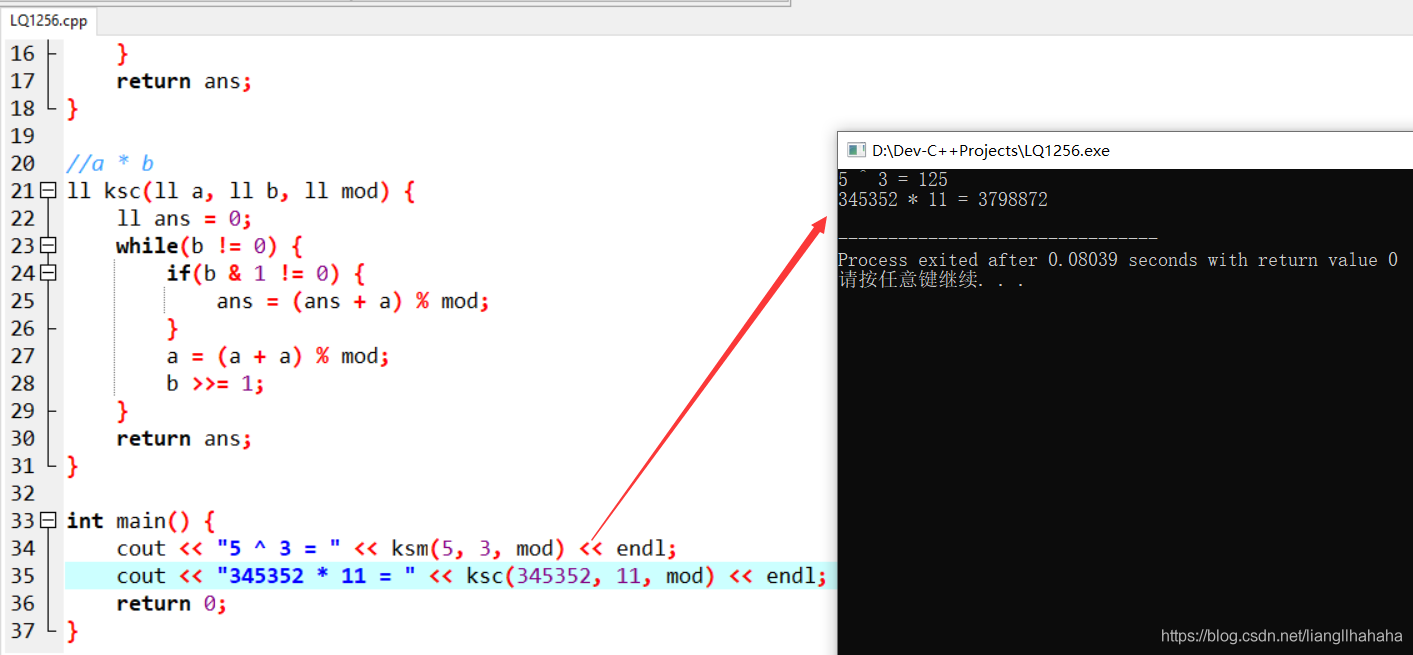
int main() {
cout << "5 ^ 3 = " << ksm(5, 3, mod) << endl;
cout << "345352 * 11 = " << ksc(345352, 11, mod) << endl;
return 0;
}
运算结果:
7 References
以上,有问题欢迎指正!